SkipList Redis Go

跳表的go语言实现

Posted by Run-dream Blog on July 14, 2021

跳表是什么?

顾名思义，跳表就是 跳 + 表，也就是 多级索引 + 链表。设计的目的是为了解决链表的快速查询的问题。

设计的基础思路就是将多层链表的思想运用到链表上，但是和二叉查找不同的地方在于跳表的索引是基于概率的。

具体的说:

  1. 假设现在有一个链表，需要查找到某个值为k的节点。只能遍历整个链表，时间复杂度为 O(n)。
  2. 在链表上让每相邻两个节点增加一个指针，让指针指向下下个节点，查找时从添加的链表上进行遍历，时间复杂度为 O(n /2 )。
  3. 利用同样的方式，可以在上层新产生的链表上，继续为每相邻的两个节点增加一个指针，添加更多的链表。查询时间复杂度为为O(logn),空间复杂度为 O(2n) = O(n)
  4. 按照上面的做法，插入/删除新数据的时候需要对新插入/删除后的所有节点进行调整，导致插入的时间复杂度编程O(n)。
  5. 事实上，我们并不不要求上下相邻两层链表之间的节点个数有严格的对应关系，所以skiplist提出为每个节点随机出一个层数。这个层数的分布满足幂次分布，也就是越大的值生成的几率越小。

借用大佬的图来描述一下插入和查找的过程：

插入

查询

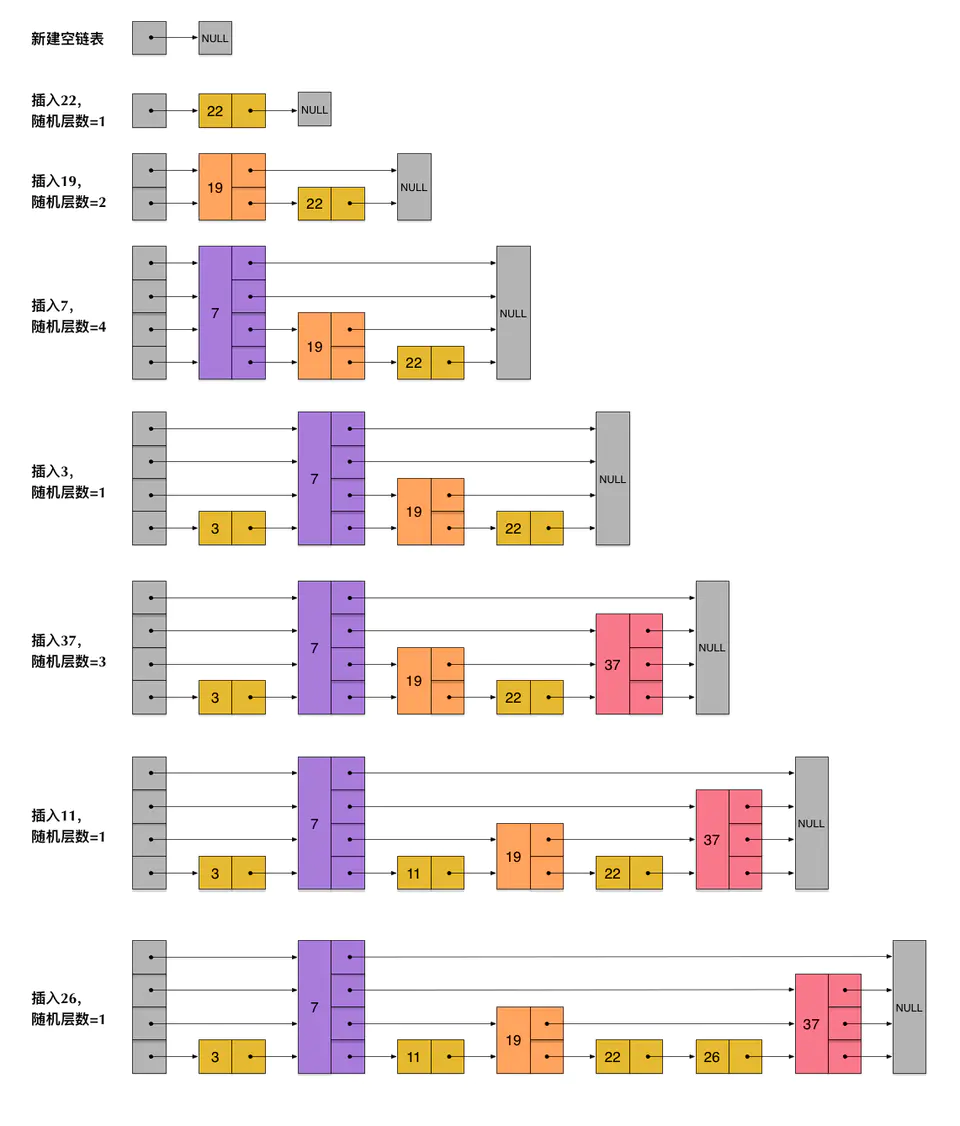
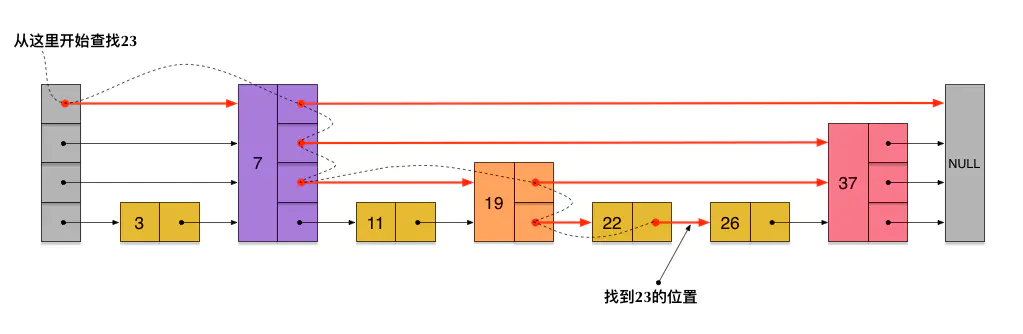
对比其他能做这件事情的数据结构，跳表有什么优势?

  • 哈希表

    哈希表不支持范围查询，查找时间复杂度接近O(1)。

  • 平衡树

    • 内存占用 通过改变概率可以节省空间
    • 范围查找 平衡树比skiplist操作要复杂
    • 算法实现难度 skiplist比平衡树要简单得多。

如何实现一个跳表？

Redis 的跳跃表实现和 William Pugh 在《Skip Lists: A Probabilistic Alternative to Balanced Trees》论文中描述的跳跃表基本相同，不过在以下三个地方做了修改：

  • 这个实现允许有重复的分值
  • 对元素的比对不仅要比对他们的分值，还要比对他们的对象
  • 每个跳跃表节点都带有一个后退指针，它允许程序在执行像 ZREVRANGE 这样的命令时，从表尾向表头遍历跳跃表。

Redis 的实现可以参考 注释后的代码。

让我们用Go来简单实现一份Redis的跳表

常量定义

// 常量
const (
	// MaxLevel 最高层数
	MaxLevel = 32
	// 每一层的晋升概率
	Probability = 0.25
)

数据结构定义

// LevelNode 索引节点
type LevelNode struct {
    // 第i层索引的下一个指针
	forward *Node
    // 对应第0层两个节点的距离
	span    int
}

// 新建索引节点
func newLevelNode() *LevelNode {
	return &LevelNode{nil, 0}
}

// Node 跳表节点结构体
type Node struct {
	// 跳表保存的关键字
	ele string
	// 用于排序的分值
	score float64
	// 后续节点
	backward *Node
	// 节点的所有索引节点
	levels []*LevelNode
}

操作实现

插入

// Insert 插入节点到跳表中
func (this *SkipList) Insert(ele string, score float64) *Node {
	if len(ele) == 0 {
		return nil
	}

	cur := this.head
	// 在各个层查找节点的插入位置，也就是目标节点的上一个节点
	update := make([]*Node, MaxLevel)
	// 用来计算span的值
	rank := make([]int, MaxLevel)
	// 遍历完以后, cur 就是之后要插入到第0层的位置的下一个节点
	for i := this.level - 1; i >= 0; i-- {
		if i < this.level-1 {
			rank[i] = rank[i+1]
		}

		for cur.levels[i].forward != nil && (cur.levels[i].forward.score < score || (cur.levels[i].forward.score == score && cur.levels[i].forward.ele < ele)) {
			rank[i] += cur.levels[i].span
			cur = cur.levels[i].forward
		}
		update[i] = cur
	}

	// 通过随机算法获取该节点层数
	level := randomLevel()

	// 如果新节点的层数比表中其他节点的层数都要大
	// 那么初始化表头节点中未使用的层，并将它们记录到 update 数组中
	// 将来也指向新节点
	if level > this.level {
		// 初始化未使用层
		for i := this.level; i < level; i++ {
			rank[i] = 0
			update[i] = this.head
			update[i].levels[i].span = this.length
		}

		// 更新表中节点最大层数
		this.level = level
	}

	// 创建一个新的跳表节点
	node := newNode(level, score, ele)
	// 将前面记录的指针指向新节点，并做相应的设置
	for i := 0; i < level; i++ {
		// 设置新节点的 forward 指针
		node.levels[i].forward = update[i].levels[i].forward
		// 将沿途记录的各个节点的 forward 指针指向新节点
		update[i].levels[i].forward = node
		// 计算新节点跨越的节点数量
		node.levels[i].span = update[i].levels[i].span - (rank[0] - rank[i])
		// 更新新节点插入之后，沿途节点的 span 值
		update[i].levels[i].span = (rank[0] - rank[i]) + 1
	}

	// 未接触的节点的 span 值也需要增一，这些节点直接从表头指向新节点
	for i := level; i < this.level; i++ {
		update[i].levels[i].span++
	}

	// 设置新节点的后退指针
	if update[0] != this.head {
		node.backward = update[0]
	} else {
		node.backward = nil
	}

	// 处理尾节点
	if node.levels[0].forward != nil {
		node.levels[0].forward.backward = node
	} else {
		this.tail = node
	}

	//更新跳表长度
	this.length++

	return node
}
删除

// Delete 删除节点
func (this *SkipList) Delete(ele string, score float64) bool {
	cur := this.head
	// 在各个层查找节点的插入位置，也就是目标节点的上一个节点
	update := make([]*Node, MaxLevel)
	// 按照索引从上向下查找节点
	for i := this.level - 1; i >= 0; i-- {
		for cur.levels[i].forward != nil && (cur.levels[i].forward.score < score || (cur.levels[i].forward.score == score && cur.levels[i].forward.ele < ele)) {
			cur = cur.levels[i].forward
		}
		update[i] = cur
	}

	node := cur.levels[0].forward
	if node != nil && node.score == score && node.ele == ele {
		this.deleteNode(node, update)
		return true
	}
	return false
}
查询
// isInRange 快速判断是否可能有节点
func (this *SkipList) isInRange(min, max float64) bool {
	if min > max {
		return false
	}
	if this.tail == nil || this.tail.score < min {
		return false
	}
	if first := this.head.levels[0].forward; first == nil || first.score > max {
		return false
	}
	return true
}

// GetRange 根据分值区间查找节点, 简化一下问题，只考虑闭区间
func (this *SkipList) GetRange(min, max float64) (begin, end *Node) {
	if !this.isInRange(min, max) {
		return nil, nil
	}
	cur := this.head.levels[0].forward
	for i := this.level - 1; i >= 0; i-- {
		for cur.levels[i].forward != nil && cur.levels[i].forward.score < min {
			cur = cur.levels[i].forward
		}
	}
	if cur.levels[0].forward == nil {
		begin = cur
	} else {
		begin = cur.levels[0].forward
	}
	cur = this.head.levels[0].forward
	for i := this.level - 1; i >= 0; i-- {
		for cur.levels[i].forward != nil && (cur.levels[i].forward.score <= max) {
			cur = cur.levels[i].forward
		}
	}
	if cur.levels[0].forward == nil && cur.score <= max {
		end = cur
	} else {
		end = cur.backward
	}
	return begin, end
}

关键算法

随机数生成

// RandomLevel 获取一个随机的层级 返回值的范围是 [1, MaxLevel]
func randomLevel() int {
	level := 1
	for rand.Float64() < Probability && level < MaxLevel {
		level += 1
	}
	return level
}

Tips

  1. 查找时，是由高层的索引一层层向下查找,而插入的时候是先随机生成level 然后在原来的各个层级找对前一节点，依次插入

  2. 随机的层级Redis是用位运算实现的

    int zslRandomLevel(void) {
    int level = 1;
   
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
   
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

完整的代码放到了github

参考文章

Redis 为什么用跳表而不用平衡树？

FEATURED TAGS
Docker Read DataBase Egg.js Linux VSCode Java 鸡汤 智识训练营 心理学 Redis git bull
FRIENDS